TL;DR — We present Sobolev Fourier Neural Operator (SoFoNO) that learns Sobolev exponents to enhance frequency-domain detail reconstruction, achieving more realistic arbitrary-scale super-resolution without attention.
Abstract
Accurately reconstructing fine textures and sharp edges remains a significant challenge in Single Image Super-Resolution (SISR) tasks, often resulting in overly smooth and less realistic images. To alleviate this issue we propose a novel SISR framework named Sobolev Fourier Neural Operator (SoFoNO). Central to our approach is a specialized architecture featuring a Sobolev Branch, which effectively captures detailed structures in the frequency domain via a learnable Sobolev exponent. Importantly, the learned Sobolev exponent is directly employed as derivative order parameters within the Sobolev loss function, enabling more precise and visually coherent reconstructions. Unlike conventional pixel-level loss functions, the Sobolev loss explicitly incorporates frequency-domain penalties, significantly enhancing the reconstruction quality of detailed image structures. Extensive experiments conducted on multiple datasets under both in-scale and out-scale scenarios demonstrate that our SoFoNO provides robust and effective performance in arbitrary-scale super-resolution, consistently outperforming representative existing methods across various tested scale factors without relying on attention mechanisms.
Demo
Changing resolution (34px → 340px)
Input

Output

Zoom-In Animation
Input Output

Multi-scale Before/After Comparison
Motivation
We utilize a practical approximation method, regardless of whether . The equation is as follows:
where represents the frequency domain variable, and denote the Fast Fourier Transform (FFT) and the Inverse Fast Fourier Transform (IFFT), respectively, and represents the derivative order.

We introduce a learnable Sobolev exponent s that directly controls frequency emphasis in the transformation. When s > 0, high-frequency components are amplified, resulting in sharper, whereas s < 0 enhances low-frequency components, producing smoother outputs.
Architecture
The proposed SoFoNO architecture consists of three main stages: Encoder, SoFoNO Blocks, and Decoder.
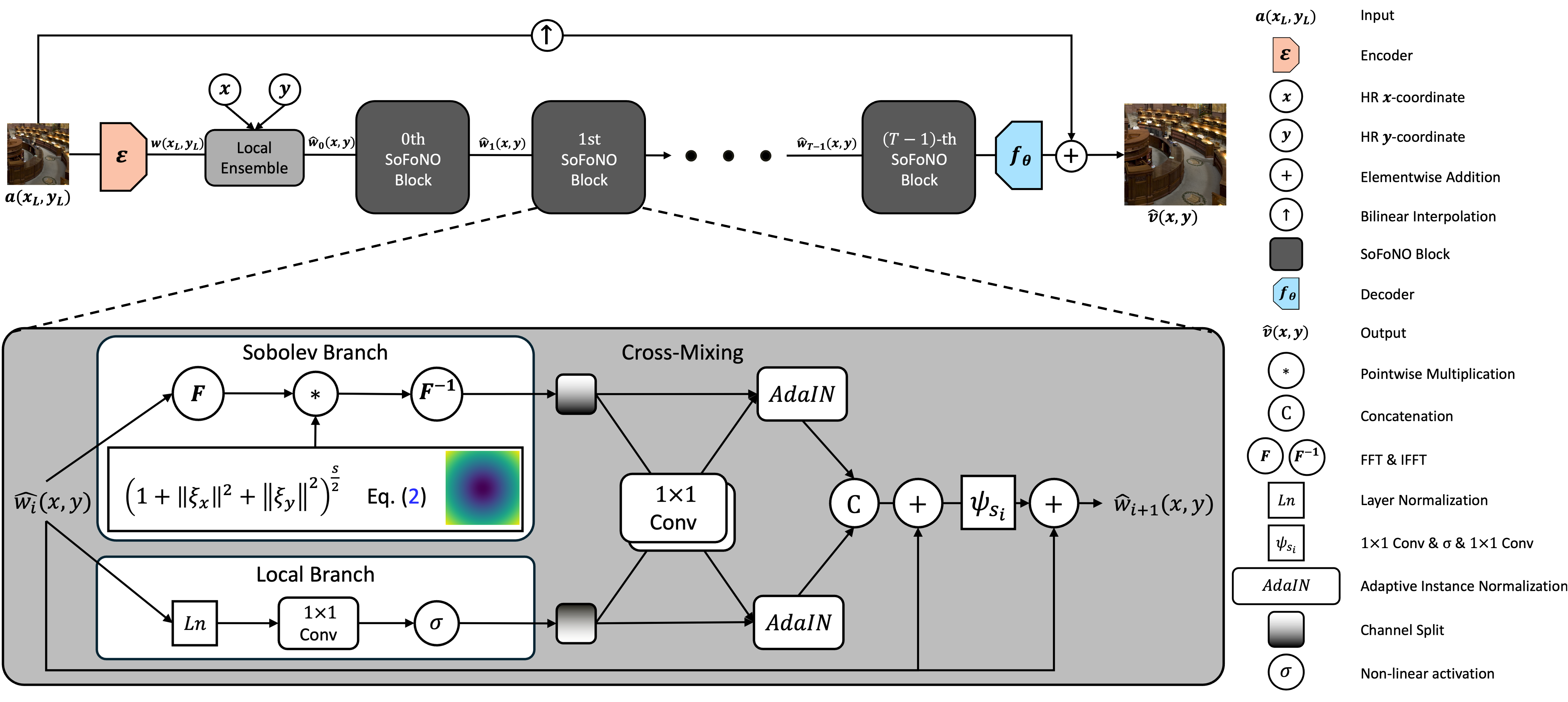
Overall Architecture of SoFoNO.
First, a low-resolution (LR) image is processed by an EDSR encoder to produce deep feature maps that capture local texture information. Then, a Local Ensemble module performs arbitrary-scale upsampling by aggregating nearby latent features with their relative coordinates, enabling flexible resolution synthesis. These features are fed into a sequence of SoFoNO Blocks, each containing two parallel branches: a Local Branch that refines spatial details and a Sobolev Branch that operates in the frequency domain to emphasize high-frequency components using a learnable Sobolev exponent. The two branches are adaptively fused through Cross-Mixing and AdaIN operations to effectively integrate spatial and spectral information. Finally, the Decoder reconstructs the high-resolution image through lightweight convolutional layers and bilinear interpolation, while a combined real- and frequency-domain loss ensures balanced optimization.
Results
Quantitative Results
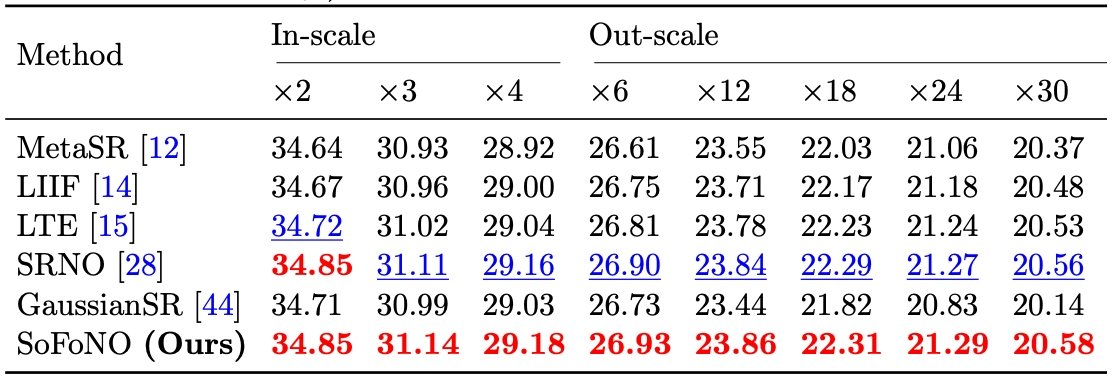
Results on the DIV2K validation set.
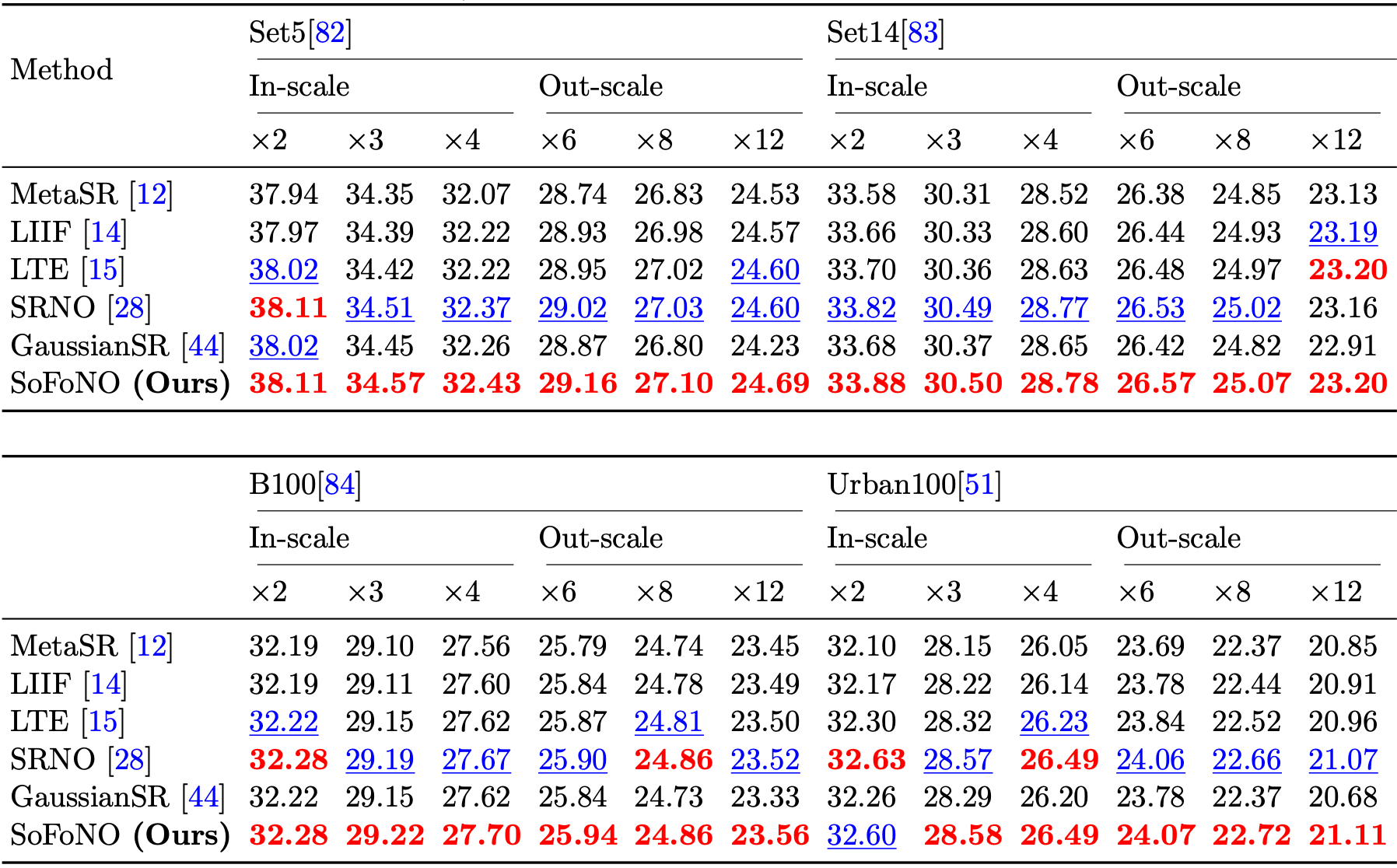
Results on the Benchmark datasets.
SoFoNO demonstrates consistently superior performance across various datasets. It achieves outstanding results on the DIV2K validation set and maintains high performance on multiple benchmark datasets, including Set5, Set14, B100, and Urban100. These results highlight SoFoNO’s strong generalization ability and its effectiveness in producing high-quality, detail-preserving reconstructions across diverse image domains.
Qualitative Results


SoFoNO demonstrates remarkable visual fidelity. The left panel (×4) shows SoFoNO’s ability to accurately reconstruct fine textures and structural patterns, preserving high-frequency details with exceptional clarity at in-scale. In contrast, the right panel (×10) highlights its robustness under out-scale conditions, where conventional methods often fail. SoFoNO faithfully restores complex structures like ceiling textures, maintaining both texture coherence and geometric consistency.
Analysis
During training, the learnable Sobolev exponent s initially takes negative values, indicating a focus on low-frequency, coarse structures. As training progresses, s gradually increases and becomes positive, shifting the model’s emphasis toward high-frequency details and resulting in sharper, more refined reconstructions.
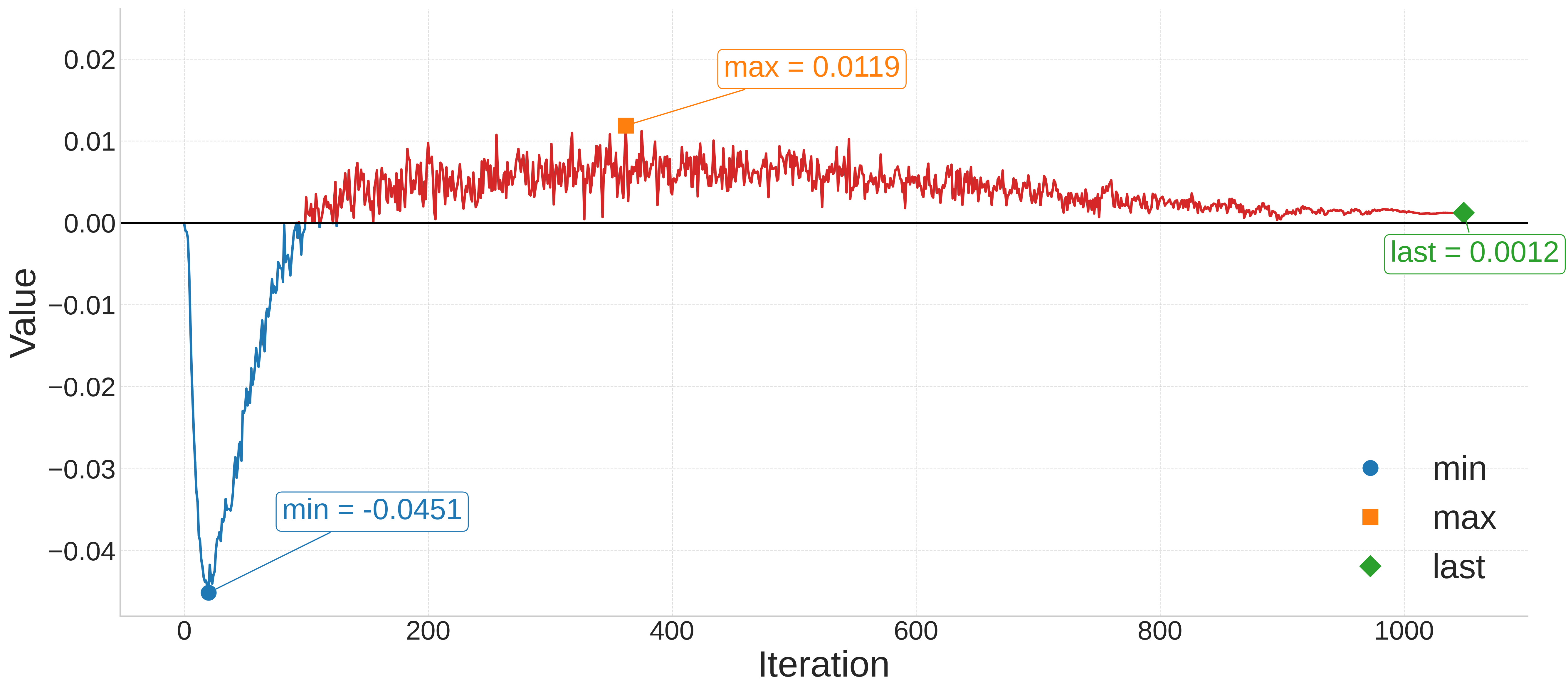
Convergence trend of parameter s in SoFoNO during training.
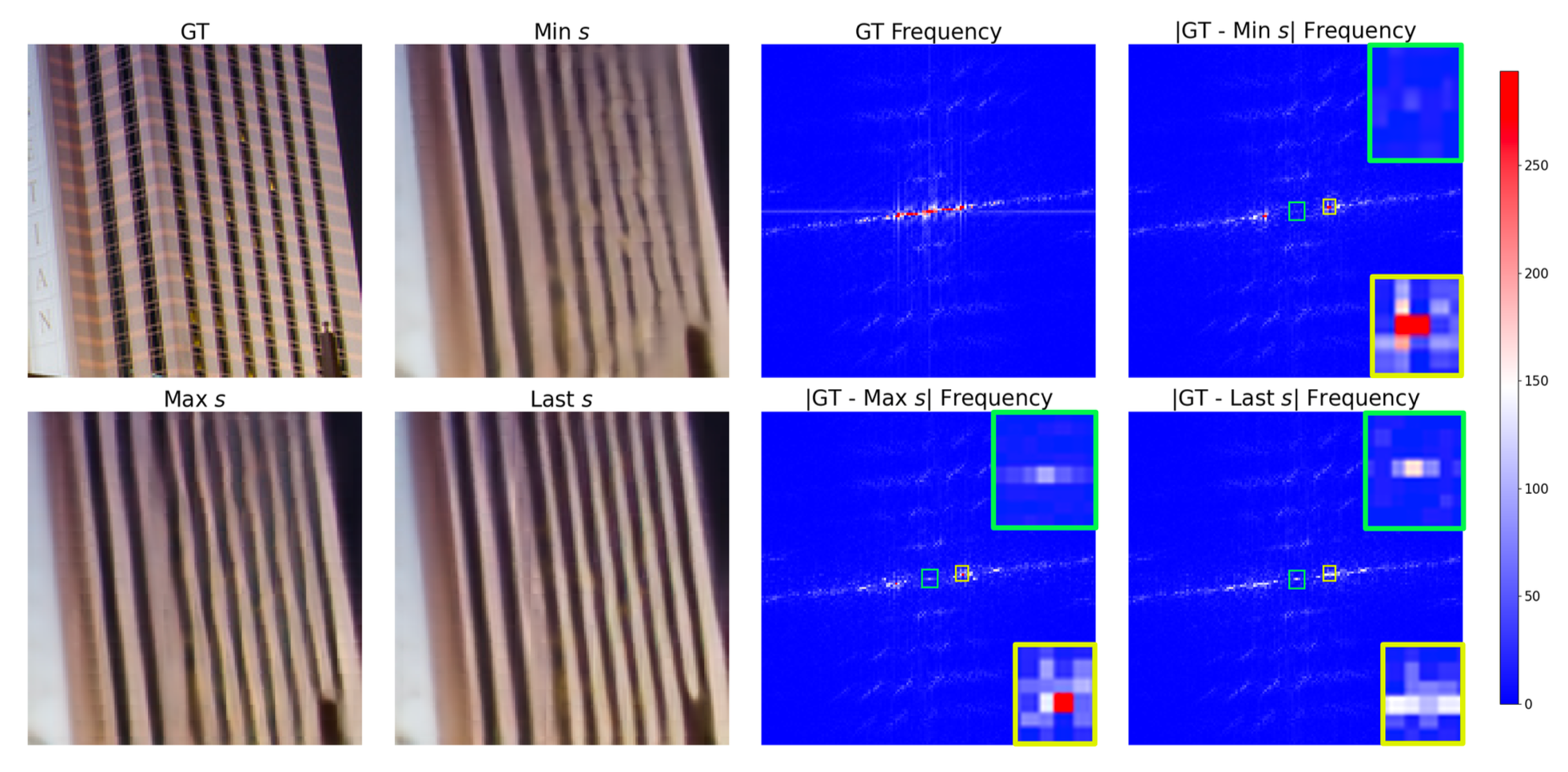
Reconstructed image (x7) patches (left) and corresponding frequency error maps (right) for different values of s.
BibTeX citation
@article{oh2025sofono, title={SoFoNO: Arbitrary-scale image super-resolution via Sobolev Fourier neural operator}, author={Oh, Jong Kwon and Son, Hwijae and Hwang, Hyung Ju and Oh, Jihyong}, journal={Neurocomputing}, pages={131944}, year={2025}, publisher={Elsevier}}